Software Developers must have coding skills, the ability to use existing software frameworks, and the ability to Google stuff and read programming language documentation.

To be a software developer (a.k.a. programmer or software engineer) today, you don’t need a degree in computer science. In fact, computer science really isn’t about “how” you develop software today at all. It’s about how we approach software problems theoretically. And to be frank, you don’t need to worry about computer science theory to be a good software developer today. You just need to know how to solve problems using code, be good at using existing software frameworks, as well as, know how to Google stuff and read programming language documentation.

However, there are some essential computer science concepts that every software developer should know. While they don’t help you develop software per se, they allow you to get better at visualizing the performance and nature of software problems, as well as, allow you to understand the terminology that coworkers with computer science degrees will use in these regards. More specifically, you should understand the following in computer science lingo:

• The difficulty/complexity of a problem
• How an algorithm scales at its inputs scale

Before we dive into these concepts, I’ll start with a basic history of computer science. Because, you should also be able to discuss the origins of your profession!

How difficult or complex is a problem in computer science?

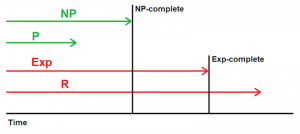
It’s important to understand how to discuss the difficulty or complexity of software development problems. In computer science, we define complexity not in the number of lines of code or the amount of caffeine needed to produce the code, but in the time it takes for a Turing Machine to solve it.

• P (polynomial time)is the time to solve a problem using a polynomial expression (involving variables, coefficients and operators). Since computers can solve the same polynomial in the same period of time, so we say that polynomial time is deterministic. Most simple problems are said to be solvable in P.
• Exp (exponential time)describes complex problems that take much longer to solve (or may never be solved), depending on the input and nature of the problem itself. They could take a few seconds to solve or a few years to solve, depending on the input. If the solution can be verified as “optimal” using a true/false polynomial expression, then we say the problem is Exp-complete. If we can’t verify it or must verify it using reduction, we say it is Exp-hard. R (recursive) problems are an example of Exp-hard.
• NP (non-deterministic polynomial time)is what we strive for when it comes to solving complex Exp problems. Think of NP as a shortcut that you take when solving an Exp problem (i.e. a stroke of inspiration) that allows you to solve it much quicker. If you are able to use a true/false polynomial expression to verify that your solution was the optimal one, then we say the problem is NP-complete. Otherwise we say it is NP-hard (i.e. we’ll assume it was the optimal one by reduction, or just look the other way). Tetris is an example of an NP-complete problem. You can solve each line quickly using a stroke of inspiration, and later watch a recording of your gameplay to determine if it was the optimal solution at the time (or write code to verify it using polynomial expressions).

How does an algorithm scale as its inputs scale?

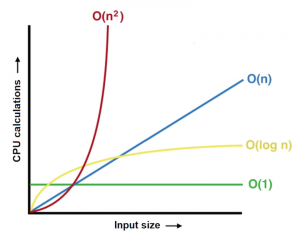
Another important concept you should be able to discuss concerns the nature of algorithms. In computer science, we use Big-Order (or Big-O) notation to describe how many CPU operations it takes to solve an algorithm based on the inputs that are provided to the algorithm.

O(1) means that the algorithm takes the same number of CPU operations to solve regardless of the input.

O(n) means that the number of CPU operations scales linearly as the input is increased.

O(n²) means that the number CPU operations scales exponentially as the inputs are increased (this should be avoided for obvious reasons). For example, an iterative search is an example of O(n²).

O(log n) means that the number of CPU operations scales logarithmically as the inputs are increased. For example, a B-tree search is an example of O(log n). O(n²) algorithms should be restructured to be O(log n) whenever possible.

Learn more about coding and software development by visiting our Applications Developer Program here.